How can I insert a signature in my PDF files?
Inserting a signature into a PDF document
1. Go to the following link:
https://www.pdfescape.com/
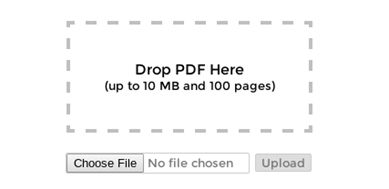
2. You need to upload your pdf file by drag and drop, or by browsing it:
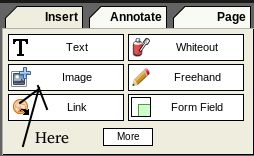
3. When the file is opened, on your left side of the screen INSERT -> Image
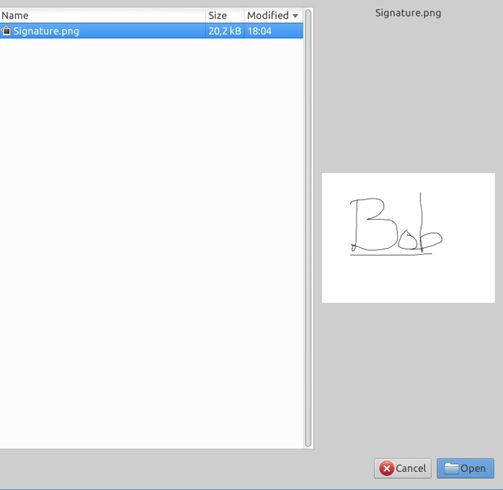
4. You then need to upload the file (SIGNATURE) you want to use:
5. When the file is uploaded, all you need to do is to select where you want to insert the Signature:
6. You can resize the image to fit the space required for the signature:
7. Adjust the size of your signature image until it fits perfectly in the signature space.
8. After the Signature is positioned and resized to fit the required space all you need to do is to save the file:
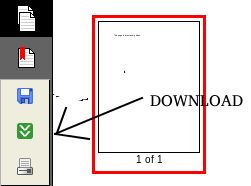
9. You can now download your signed PDF file: